Let’s talk about stats (2).

Il y a pas mal de temps, j’avais écrit ce billet sur les essais de non infériorité, et les risques de mauvaise interprétation clinique induits par leurs spécificités statistiques.

Depuis, j’ai lu plusieurs articles qui m’ont permis de corriger et d’affiner très partiellement mes idées sur le sujet.

Comme j’ai constaté que le théorème de Bayes vous a intéressé, et que la compréhension d’un minimum sur les statistiques biomédicales me semble fondamental pour optimiser sa pratique médicale, je vais donc essayer de faire une petite note de synthèse sur ce sujet.

Comme d’habitude, n’hésitez pas à commenter pour critiquer et enrichir le sujet.

 

Un test de « non infériorité » permet, comme le précisent Michel Cucherat et Eric Vicaut « de montrer que l’efficacité d’un nouveau traitement n’est pas trop inférieure à celle du traitement de référence, mais pas de conclure à la stricte équivalence d’efficacité ».

 

Imaginons une maladie X qui possède un paramètre mesurable pertinent pour l’évaluation de son pronostic.

Imaginons un traitement de référence, R, parfaitement connu (il a donc notamment été testé avec succès contre un placebo), et un traitement nouveau N en cours d’évaluation.

 

Comment comparer ces deux traitement R et N ?

Il suffit de faire un test d’hypothèses pour tester leur différence D.

C’est le choix de ces hypothèses H0 et H1 (l’hypothèse alternative) qui va déterminer le type de l’essai

 

Pour les essais de non infériorité, les deux hypothèses sont les suivantes :

 

H0 : risque absolu de différence ≥marge

H1 : risque absolu de différence <marge

La non infériorité est acceptée si la limite supérieure de l’intervalle de confiance de la différence D est strictement inférieure à la limite supérieure de cette marge, ce qui est le cas dans l’exemple suivant:

 

 

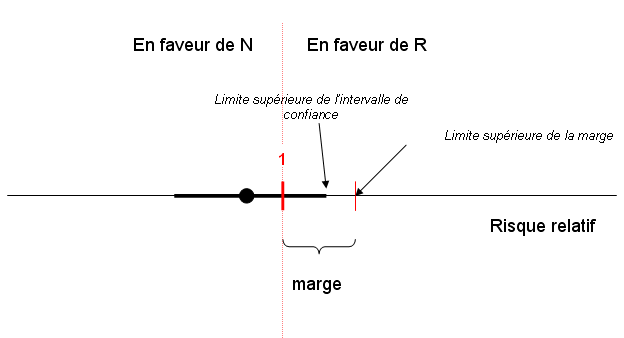
Le choix de cette marge est donc un préalable absolument fondamental. Plus la marge est importante, et plus l’essai a de chances d’être « positif » pour N, mais au prix d’accepter une différence cliniquement inacceptable entre N et R.

Le malheur est qu’il n’existe pas de moyen statistique univoque pour le faire. Ce sont des critères « cliniques », et les résultats des essais préalables qui permettent de l’estimer.

Il existe tout de même un « consensus » qui oriente ce choix : la marge doit être environ égale à 50% d’une valeur égale à 95% du risque absolu de la différence entre R et un placebo.

 

Par exemple, prenons l’essai ONTARGET qui compare le telmisartan et le ramipril chez des patients à haut risque cardio-vasculaire.

Le risque relatif du ramipril par rapport au placebo dans l’étude HOPE était de 0.775. Les auteurs de ONTARGET ont choisi le 40ème percentile de cette valeur, soit 0.794 « afin de mieux estimer » l’effet du ramipril. Cela donne une valeur du risque relatif de 1.26 (soit 26% d'augmentation du risque relatif). Les auteurs de ONTARGET ont donc choisi comme marge la valeur égale à 50% de ce risque, soit 1.13 (13%).

A posteriori, ONTARGET a permis d’observer le résultat suivant :

 

 

 

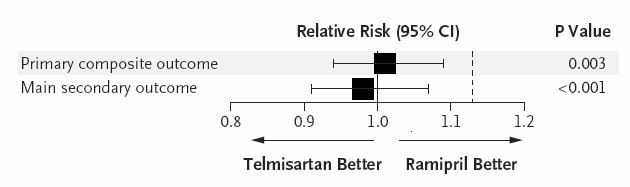
Soit une différence maximale potentielle d’efficacité de 9% (borne supérieure de l’intervalle de confiance à 1.09).

 

Quoiqu’il en soit, malgré cela, les auteurs et les « leaders d’opinion » ont conclu que les deux traitements étaient identiques :

 

 

 

 

(numéro d'avril 2008 de "Consensus Cardio News")

 

Mais vous comprenez maintenant pourquoi on ne peut pas conclure à une stricte équivalence d’un point de vue statistique, car on tolère toujours dans ces essais un certain degré de perte d’efficacité.

Par contre, les cliniciens ont bien voulu sacrifier un peu d’efficacité du ramipril (potentiellement jusqu’à 9%, donc) contre une meilleure tolérance clinique pour le telmisartan et conclure in fine en « l’équivalence » des deux produits

Mais quand on veut promouvoir un article ou un produit, vaut mieux ne pas s’embarrasser de telles subtilités qui pourraient faire réfléchir le lecteur-prescripteur.

 

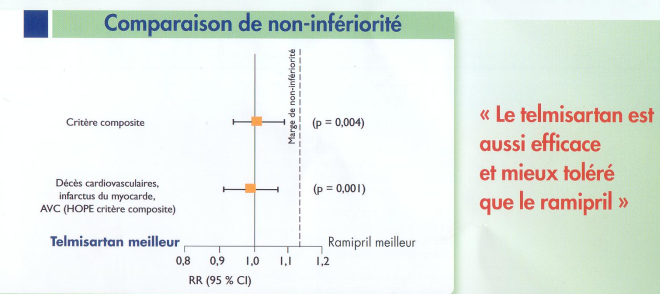
(même numéro d'avril 2008 de "Consensus Cardio News")

"Le telmisartan est aussi efficace (vrai si l'on accepte, justement la possibilité d'une perte  partielle d'efficacité...) et mieux toléré que le ramipril (peut-être vrai, mais la tolérance n'était ni un critère primaire, ni un critère secondaire de ONTARGET)". Evidemment, vu comme cela, le slogan devient alors beaucoup moins sexy...

 

J’ai pris ONTARGET comme premier exemple, car l’ensemble de la communauté scientifique le considère comme un « bon » essai de non-infériorité.

Maintenant, nous allons considérer une série de « mauvais » essais, la série des essais SPORTIF.

Le programme de recherche SPORTIF comparait l’efficacité de la warfarine, un antivitamine K, et le ximelagatran un inhibiteur de la thrombine dans la prévention des accidents thrombo-emboliques chez des patients en fibrillation auriculaire.

La warfarine étant le traitement de référence, le ximelagatran étant le traitement alors en cours d’évaluation. Ne le cherchez pas en pharmacie, ce traitement a été retiré du marché quelques années plus tard pour un problème de toxicité hépatique.

Ce superbe article dissèque en détail ce programme, et notamment critique sévèrement la méthodologie des essais de non-infériorité.

Les auteurs de SPORTIF sont partis d’un taux d’événements thrombo-emboliques annuels de 3.1% pour la warfarine et d’une marge de non infériorité de 2% pour la différence absolue.

Si les auteurs avaient appliqué la règle communément admise des 50% dont j’ai parlé plus haut, ils auraient dû prendre une marge de 1%.

1%, 2%, cela peut sembler peu. Mais nous raisonnons en terme de différence absolue.

Si l’on considère la différence relative tolérée par les auteurs, on obtient une marge qui est au maximum de 1.65, soit près de 65%.

Autrement dit, les concepteurs de ces essais ont estimé que le ximelagatran sera « équivalent » à la warfarine, même si cette dernière est 65% plus efficace.

Pourtant, ces essais ont été publiés dans des journaux prestigieux, le Lancet, le JACC et le JAMA.

La conclusion des auteurs de l’article publié dans le Lancet est d’ailleurs tout à fait claire :

 

 

 

 

Et la subtilité du choix de la marge, qui n'en est pas une, a été « expédiée » en 2 lignes dans l’analyse statistique :

 

 

 

 

A l’époque, les réactions ont été dithyrambiques, par exemple de la part d’un très grand nom de la cardiologie française (mondiale) le 02/04/03 :

 

« Session chair Dr Jean-Pierre L B*** (University Hospital of Besanon [sic], France) called these results a "major breakthrough" for patients with AF. "No titration, fixed dose, no control of blood coagulation is definitely a major success, a major breakthrough, and we are all eagerly awaiting the results of the SPORTIF V trial." » (source : theheart.org, voir dans les références)

 

Permettez moi cette aparté qui n'a strictement rien à voir avec le sujet, mais il est toujours très très drôle, bien qu’un peu facile et un peu cruel de rechercher sur le net les déclarations péremptoires faites à l’époque par nos grands leaders d’opinion sur telle ou telle molécule qui a fait quelques mois ou années après un flop médical retentissant.

Autre exemple du 19/03/2005, pris au hasard (même source, ici) :

 

« "Le message de RIO Europe qui recoupe celui de RIO NA est que la perte de poids se maintient, de même que la perte du tour de taille et les effets secondaires après une longue période sont pratiquement inexistants. Ils surviennent dans les premières semaines voire mois puis ils s'abaissent" a indiqué le Pr Jean-Pierre B*** à Heartwire (Centre Hospitalier Jean Minjoz, Besançon). ».

(Pour rappel, la dernière mise en garde du 05/08/08 de l’Afssaps concernant le Rimonabant.)

 

 

Mais je m’égare, revenons à nos moutons.

 

 

Par ailleurs, les auteurs de l’article du JACC estiment à 1.9% plutôt qu’à 3.1% le nombre d’évènements annuels sous warfarine selon des séries « historiques ». Ils accusent donc aussi les auteurs des essais SPORTIF d’avoir sous-estimé de près de 50% l’efficacité de la warfarine, afin, bien entendu de favoriser le ximelagatran.

Heureusement que la FDA a des experts en statistiques, car l'intervalle de 2% a quand même fait tiquer l'agence. Finalement, l'hépatotoxicité (à cette époque supposée) du ximelagatran et ces fameux 2% font faire retoquer la demande d'extension d'AMM du laboratoire concernant la fibrillation auriculaire. C'est cette même hépatotoxicité qui va finalement conduire au retrait définitif de ce produit le 13/02/2006.

 

Autrement dit, un médecin qui fait uniquement confiance à l’information parcellaire ne reprenant que la conclusion de l’article, une information généreusement apportée (pas donnée) par l’industrie pharmaceutique ou des leaders d’opinion n’a absolument aucune chance de pouvoir avoir une réflexion critique dessus.

Un médecin « lambda » qui a la volonté de lire l’article n’aura que peu de chance de mettre en cause la conclusion.

Seul un médecin avec une solide culture statistique et beaucoup de temps devant lui pourra critiquer cet article. Dans l’immense majorité des cas, ce médecin n’est pas prescripteur.

 

Je tire de tout cela deux conclusions et demi.

Primo, je jette à la poubelle de façon systématique tout article qui n’est pas de supériorité, tant leur analyse me semble complexe. Complexité à la hauteur des possibilités de bidouillage de la part des auteurs.

Secundo, il est très difficile d’être à la fois prescripteur et capable d’analyser les données scientifiques sur lesquelles, pourtant, se basent nos prescriptions.

Secundo et demi, je n’écoute jamais les leaders d’opinion.

 

 

 

Ajout du 25/08/08: merci à JPJ d'avoir relu mon texte et de m'avoir envoyé par mail ses corrections éclairées

 

°0°0°0°0°0°0°0°0°0°

 

Références:

 

Vicaut E, Cucherat M. Essais de non-infériorité : quelques principes simples. Presse Med. 2007 Mar;36(3 Pt 2):531-5. Epub 2007

 

The ONTARGET Investigators. Telmisartan, Ramipril, or Both in Patients at High Risk for Vascular Events. N Engl J Med. 2008 Apr 10;358(15):1547-59

 

Kaul S, Diamond G, Weintraub W .. Trials and Tribulations of Non-InferiorityThe Ximelagatran Experience. Journal of the American College of Cardiology , Volume 46 , Issue 11 , Pages 1986 - 1995

 

Executive Steering Committee on behalf of the SPORTIF III Investigators. Stroke prevention with the oral direct thrombin inhibitor ximelagatran compared with warfarin in patients with non-valvular atrial fibrillation (SPORTIF III): randomised controlled trial. The Lancet, Volume 362, Issue 9397, 22 November 2003, Pages 1691-1698

 

Susan Jeffrey. SPORTIF III: Ximelagatran as effective as warfarin to prevent stroke in AF. theheart.org. [HeartWire > News]; Apr 2, 2003. Accessed at http://www.theheart.org/article/256561.do on Aug 24, 2008

 

 

°0°0°0°0°0°0°0°0°0°0°0°

 

 

Pour aller plus loin sur les essais de non-infériorité :

 

 

Kleist P. Dix exigences aux études d’équivalence thérapeutique ou Pourquoi absence de preuve d’une différence ne signifie pas la même chose qu’équivalence. Forum Med Suisse 2006;6:814–819

 

Un éditorial trouvé dans la revue Minerva.

 

Mismetti P, Laporte S, Cucherat M. Les essais de non-infériorité. Médecine thérapeutique. Volume 13, Numéro 4, Juillet-Août 2007 (accès payant)

 

La lecture critique des essais cliniques par Michel Cucherat, un polycopié disponible ici (son sujet dépasse largement les essais de non-infériorité).

 

Pour les geeks fanatiques de ce type d’essais, une page permettant d’estimer le nombre de patients à inclure dans un essai de non infériorité en fonction de différents paramètres.