Guerre et guerre.

Quelle aberration cette guerre, comme toutes les guerres à vrai dire.

Je ne vois pas qui va pouvoir arrêter l’ours russe alors que les défenses géorgiennes cèdent de toute part. Les efforts de paix de la communauté internationale me semblent bien vains dans cette situation. Cela me rappelle une phrase de Pompée: « Ne cesserez-vous pas de nous alléguer vos lois, à nous qui portons l'épée ? »

Ces deux photos du NYT résument parfaitement l’inhumanité de ce conflit.

Je pense aussi à tous nos confrères et aux infirmières qui doivent en ce moment faire leur travail dans des conditions épouvantables.

 

David Mdzinarishvili/Reuters

 

 

Denis Sinyakov/Reuters

 

 

 

°0°0°0°0°0°0°0°0°0°

 

 

 

International / Europe

Russian Ground Forces Assault Vital Georgian City

By ANNE BARNARD

The New york Times

Published: August 11, 2008

Russian troops advanced on the city of Gori in central Georgia on Sunday night, for the first time directly assaulting a Georgian city with ground forces.

 

Stanley Kubrick for LOOK Magazine

 

Source: Bibliothèque du Congrès

 

°0°0°0°0°0°0°0°0°0°

 

 

 

(Source)

"Look Dave, I can see you're really upset about this.

I honestly think you ought to sit down calmly, take a stress pill, and think things over."

Let’s talk about stats.

 

Je vais essayer de faire une petite synthèse sur le théorème de Bayes, sans rentrer dans une théorie qui m’est largement imperméable, c'est à dire en restant pratique.

 

 

D’abord, les présentations.

Je vais m’intéresser exclusivement à l’étude de la performance d’un test médical de dépistage T d’une maladie M.

 

T peut être positif (T+), ou négatif (T-)

Un sujet peut être atteint par la maladie (M+) ou sain (M-)

 

 

 

	M(+)	M(-)
T(+)	VP	FP
T(-)	FN	VN

 

 

VP= vrai positif, FP= faux positif, VN= vrai négatif, FN= faux négatif

 

La sensibilité Se est la capacité d’un test à identifier correctement les sujets malades.

Se= VP/ (VP+FN)

 

La spécificité Sp est la capacité d’un test à identifier correctement les sujets sains.

Sp= VN/ (VN+FP)

 

Note : pour déterminer qui est malade et qui ne l’est pas, il a fallu utiliser une méthode indiscutable (on verra que c’est justement un point discutable en pratique) et indépendante du test T. On peut alors disposer de deux populations « indiscutables » : les sujets sains et les sujets malades.

 

Ca va pour l’instant ?

Allez respirez un grand coup, ça se complique un peu.

 

Malheureusement, du moins pour la simplicité, la vie n’est pas blanche ou noire, il y a beaucoup de gris.

C’est pareil pour les tests médicaux.

 

L’ensemble des individus d’une population donnée n’aura pas un même résultat du fait de la variabilité biologique.

Ces résultats vont se distribuer selon la loi normale de Laplace-Gauss, et donner une belle courbe de Gauss (qui aurait pu s’appeler courbe de Laplace, sans ce maudit allemand !).

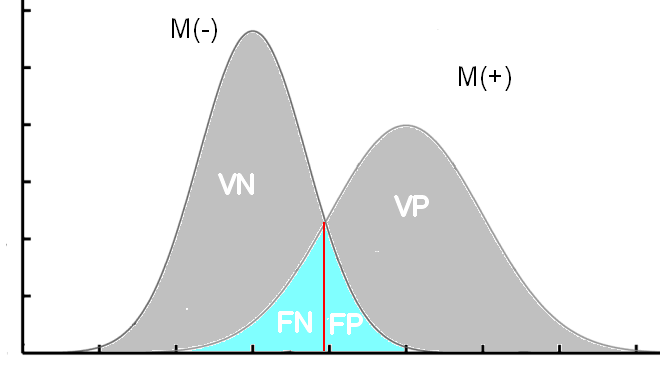
Quand on compare deux populations, les malades M(+) et les sains M(-), il y a de grandes chances que les deux courbes se croisent.

C'est-à-dire qu’il va falloir déterminer un seuil qui permettra de déterminer des sujets T(-) ou T(+).

 

 

C’est là que ça se complique, car déterminer ce seuil (en rouge sur les courbes) est une délicate question d’équilibre entre la sensibilité et la spécificité. Il va falloir choisir de privilégier l’une ou l’autre.

Plus le seuil est bas, plus on va diminuer le nombre de FN (on va donc augmenter la sensibilité), mais on va aussi augmenter le nombre de FP, et donc diminuer la spécificité.

 

 

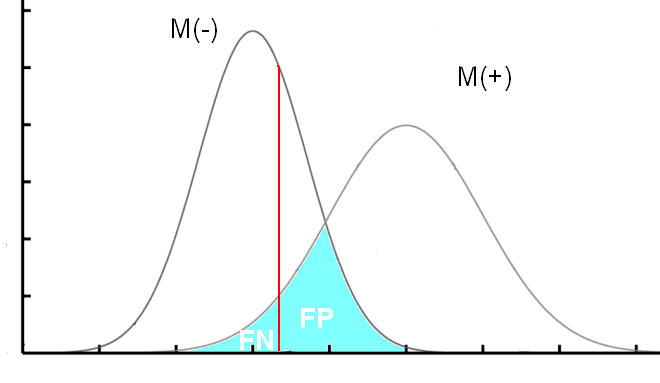
Je ne vais pas rentrer dans les détails, mais ce choix dépend de ce que l’on veut faire du test, c'est-à-dire si on veut le rendre très spécifique ou au contraire très sensible. On peut aussi déterminer ce seuil à l’aide d’une courbe « ROC » (Receiver Operating Charactéristics).

Mais sachez que le choix d’un seuil de positivité d’un test est délicat, complexe et parfois sujet à caution.

 

Dans la vie réelle, le patient et son médecin se fichent un peu de savoir quelle est la sensibilité, la spécificité d’un test, ou si sa courbe ROC est sexy.

Ce qu’ils veulent savoir c’est

Quelle est la probabilité d’être malade quand le test est positif, c’est à dire la valeur prédictive positive (VPP)?

Quelle est la probabilité d’être sain quand le test est négatif, c’est à dire la valeur prédictive négative (VPN)?

 

C’est là qu’intervient le théorème de Bayes (qui aurait pu s’appeler théorème de Laplace, sans ce maudit anglais !).

 

Pr est la prévalence de la maladie dans la population, c'est-à-dire la proportion de la maladie dans une population définie, à un instant t

Pr = nombre de cas observés à un instant t /population à risque au même instant t

 

 

VPP = (Se*Pr) / (Se*Pr)+(1-Sp)*(1-Pr)

VPN = (Sp*(1-Pr)) / (Sp*(1-Pr) + (1-Se)*Pr)

 

Deux « grosses » formules que seuls les étudiants en médecines qui doivent passer des examens/concours déterminants pour leur vie arrivent à retenir plus de quelques heures.

Mais on peut essayer d’analyser ces formules sans faire de méningite ou déclencher une migraine.

 

On constate que la VPP et la VPN d’un test dépendent de la prévalence de la maladie.

Plus la prévalence est élevée, plus la VPP est élevée, et plus la VPN est faible.

Plus la prévalence est faible, plus la VPP est faible, et plus la VPN est élevée.

 

Ca, c’est fondamental à comprendre pour notre pratique quotidienne, presque aussi important que le « primum non nocere » (j’exagère un peu).

 

Autrement dit, si l’on effectue un test dans une population où la prévalence de la maladie est faible (dans une population à faible risque, pour exprimer les choses autrement) la probabilité qu’un patient avec un test positif soit effectivement malade sera faible, voire très faible. Au contraire, la probabilité qu’un patient soit sain en ayant un test négatif sera très élevée.

Un même test aura donc une performance variable en fonction de la population étudiée.

Si je fais une série d’épreuves d’effort à la recherche d’une coronaropathie aux enfants d’une crèche, un test positif sera peu inquiétant, un test négatif très rassurant.

Si je fais les mêmes épreuves d’effort à la recherche de la même chose dans une population d’hommes dépassant la cinquantaine, hypertendus, tabagiques et diabétiques non traités, un test positif sera très probablement révélateur d’une coronaropathie latente, alors qu’un test négatif sera finalement peu rassurant.

 

Vous comprenez donc que la performance d’un test est très variable selon le patient à qui on le fait passer. Donc, en corollaire, l’interprétation qu’en fait le médecin doit être adaptée à chaque patient.

C’est difficile à imaginer, mais c’est ainsi: la performance d’un test dépend d’un paramètre qui lui est totalement étranger, la prévalence d’une maladie dans une population.

(moi, cette notion m’a toujours fasciné)

 

En général, c’est à ce point précis que j’entrevois qu’une bonne partie des examens que l’on me demande, bien que rémunérateurs, sont peu informatifs d’un point de vue statistique.

Prenons l’épreuve d’effort.

Selon cette source, sa sensibilité est environ de 68%, sa spécificité environ de 77%.

Selon cette autre source, la prévalence d’une coronaropathie diagnostiquée à l’angiographie coronaire dans une population générale de 40 à 70 ans est de 7.4%.

Il faut se méfier de jouer à l’apprenti sorcier avec les chiffres, mais cela donne une VPN à 96.79% et une VPP à 19.11%. Ce cas illustre bien le manque de pertinence d’une épreuve d’effort positive dans une population à relativement faible risque.

 

Dans une population d’insuffisants rénaux à très haut risque, ce papier évalue la prévalence d’une coronaropathie à 53.3%

On obtient alors une VPN à 67.83% et une VPP à 77.14%.

On se rend compte ici que l’épreuve d’effort est ici finalement assez peu pertinente (et encore, je ne tiens pas compte des faibles capacités fonctionnelles musculaires des insuffisants rénaux en stade terminal, diminuant d’autant les performances du test d’effort).

 

Dans un nombre non négligeable de cas, on se trompe par excès ou défaut.

 

Vous comprenez donc aussi le paradoxe (apparent) de l'anesthésiste et du cardiologue qui demandent en pré-opératoire un test d'effort pour se rassurer chez un patient à très haut risque cardio-vasculaire. Plus le risque du patient est élevé, et plus la probabilité d'être faussement rassuré par un test négatif est forte. Le "Je l'endors (ou "tu peux l'endormir") tranquille car l'épreuve d'effort est rassurante" prend alors toute sa saveur...

Bien évidemment, en pratique il faut faire une épreuve d'effort avant une chirurgie lourde pour un patient à haut risque. Mais contrairement à ce que l'on croit, c'est plutôt pour sa capacité à dépister une coronaropathie qu'à être "rassuré" avant l'intervention.

 

 

Deuxième conséquence de la formule, un peu plus intuitive, celle-çi :

 

La valeur prédictive d’un test dépend de sa spécificité et de sa sensibilité.

Plus la Sp est élevée, plus la VPP est élevée.

Plus la Se est élevée, plus la VPN est élevée.

 

Ici, pas trop de soucis, la pertinence d’un test est directement dépendante de ses caractéristiques propres.

 

Tout cela pour ça, me direz vous…

Cette loi a été décrite par le révèrent Bayes à la fin du XVIIIème, mais sa non compréhension induit au quotidien des demandes statistiquement aberrantes d’examens complémentaires et aussi et surtout des interprétations tout aussi aberrantes que dangereuses pour le patient. Ce ne sont pas tellement les tests qui posent problème, mais plutôt la population dans laquelle ils sont effectués et l'interprétation qu'en fait le médecin demandeur.

Quoique…

Cette note de Jean Daniel Flaysakier évoque un commentaire publié dans le prestigieux magazine Nature sur la fiabilité des tests utilisés pour lutter contre le dopage sportif.

Bien que Donald Berry, l’auteur (un statisticien) a été rétribué par la défense d’un athlète suspecté de dopage en 1996 (merci la déclaration de conflits d’intérêts), son texte apporte un point de vue assez différent de « l’idée commune » qui prévaut sur le sujet.

Faites vous votre opinion.

 

 

°0°0°0°0°0°0°0°0°0°0°0°0°

 

 

Une fois n’est pas coutume, une petite modification de dernière minute.

Stéphane a aussi évoqué le dopage, mais cette fois en terme d’efficacité dans cette note. Je l’avais lue, mais sur le coup je n’y avais pas pensé. Merci de l’avoir rappelé dans ton commentaire !